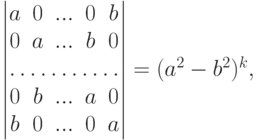НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 2: Вычисление определителей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3976 / 716 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 62 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Пример 6.8.10 (вычисление определителя n-го порядка с помощью рекуррентного соотношения). Найти определитель

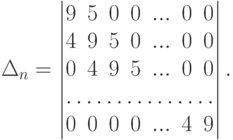
$\Delta_n = \begin{vmatrix} 9 & 5 & 0 & 0 & ... & 0 & 0\\ 4 & 9 & 5 & 0 & ... & 0 & 0\\ 0 & 4 & 9 & 5 & ... & 0 & 0\\ \hdotsfor{7}\\ 0 & 0 & 0 & 0 & ... & 4 & 9 \end{vmatrix}.$

Разложим определитель по первой строке:

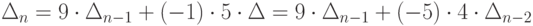
$\Delta_n = 9 \cdot \Delta_{n-1} + (-1)\cdot 5\cdot \Delta = 9\cdot \Delta_{n-1} + (-5) \cdot 4\cdot \Delta_{n-2}$

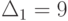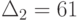(в соответствующем миноре $\Delta$ мы применим разложение по первому столбцу). Если учесть, что $\Delta_1=9$ и $\Delta_2=61$ , полученная рекуррентная формула позволяет вычислить 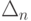$\Delta_n$ для любого n. Нетрудно убедиться, что 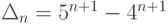$\Delta_n = 5^{n+1}-4^{n+1}$ (это можно доказать, например, индукцией по n ).

Задача 6.8.11.Вычислить определители порядка n :

а)

$\begin{vmatrix} 0 & ... & 0 & 1\\ 0 & ... & 1 & 0\\ \vdots & \revddots & & \vdots\\ 1 & 0 & ... & 0 \end{vmatrix}$

(все элементы вне побочной диагонали равны 0, а на побочной диагонали стоят 1 ).

б)

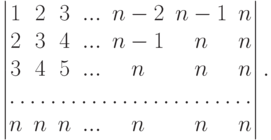
$\begin{vmatrix} 1 & 2 & 3 & ... & n-2 & n-1 & n\\ 2 & 3 & 4 & ... & n-1 & n & n\\ 3 & 4 & 5 & ... & n & n & n\\ \hdotsfor{7}\\ n & n & n & ... & n & n & n \end{vmatrix}.$

Упражнение 6.8.12 (игра в определитель). Играют два участника, расставляя по очереди числа 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторений в качестве элементов матрицы $3\times 3$ . Один из участников (I) стремится в итоге получить положительный определитель, а другой (II) - отрицательный. Чтобы уравнять шансы, играется две партии: в первой партии первый ход делает участник I, а во второй - участник II. После этих двух партий значения полученных определителей складываются. Если получилось положительное число, то выиграл участник I, если отрицательное число, то выиграл участник II, если нуль, то ничья. Покажите, что сумма всех 9! определителей, возможных в этой игре, равна нулю.

Теорема 6.8.13 (об определителе с углом нулей).

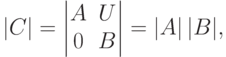
$|C| = \begin{vmatrix} A & U\\ 0 & B \end{vmatrix} = |A|\,|B|,$

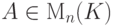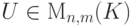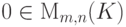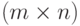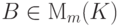где $A\in \mM_n(K)$ , $U\in\mM_{n,m}(K)$ , $0\in \mM_{m,n}(K)$ - нулевая $(m\times n)$ -матрица, $B\in \mM_m(K)$ .

Доказательство. Проведем индукцию по n. Начало индукции n=1 рассмотрено в лемме 6.8.3. Пусть $n \geq 2$ и утверждение верно для всех n'<n. Разложим наш определитель |C| по первому столбцу: |C|=a_{11}C_{11}+...+a_{n1}C_{n1}. Так как по индуктивному предположению для M_i1

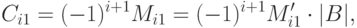
$C_{i1} = (-1)^{i+1}M_{i1}=(-1)^{i+1}M'_{i1}\cdot |B|,$

где

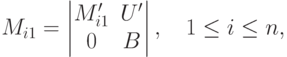
$M_{i1} = \begin{vmatrix} M'_{i1} & U'\\ 0 & B \end{vmatrix},\quad 1 \leq i \leq n,$

M'_{i1} - дополняющий минор элемента a_{i1} в матрице A, то

$\begin{mult} |C| = \sum_{i=1}^{n}a_{i1}C_{i1}=\sum_{i=1}^{n}a_{i1}(-1)^{i+1}M'_{i1}|B|={}\\ {}=\smash[t]{\biggl(\,\sum_{i=1}^{n}a_{i1}A_{i1}\biggr)}|B|=|A|\,|B|. \end{mult}$

Следствие 6.8.14. Пусть A_i, 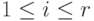$1 \leq i \leq r$ , - квадратные матрицы. Тогда

$\begin{vmatrix} A_1 & & & \lefteqn{\raisebox{-5pt}[0pt][0pt]{\text{\hspace*{-15pt}\Large 0 }}}\\ & A_2\\ & & \ddots\\ \lefteqn{\raisebox{5pt}[0pt][0pt]{\text{\hspace*{5pt}\Large 0 }}} & & & A_r \end{vmatrix} = |A_1| \, |A_2| ... |A_r|.$

Упражнение 6.8.15 (теорема Лапласа). Если M - минор (т. е. определитель матрицы), проходящий через k строк с номерами i₁,...,i_k и k столбцов с номерами j₁,...,j_k, $k \geq 1$ , то дополнительный минор $\bar M$ определяется как определитель, получаемый вычеркиванием строк i₁,...,i_k и столбцов j₁,...,j_k. Алгебраическое дополнение минора M определяется следующим образом:

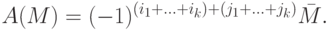
$A(M)=(-1)^{(i_1+...+i_k)+(j_1+...+j_k)}\bar M.$

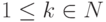Если $A=(a_{ij})\in\mM_n(K)$ , $1 \leq k \in N$ , i₁,...,i_k - зафиксированные номера k строк, то определитель |A| равен сумме всех произведений MA(M), где M пробегает все C_n^k

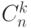миноров, проходящих через строки с номерами i₁,...,i_k.

Частными случаями теоремы Лапласа являются теорема о разложении по строке ( k=1 ) и теорема об определителе с углом нулей.

Теорема 6.8.16 (правило Крамера). Для квадратной системы линейных уравнений $(a_{ij}\mid b_i)$ с $(n\times n)$ -матрицей A=(a_{ij}) имеем:

система является определенной тогда и только тогда, когда $|A|\neq 0$ ;
в этом случае (т. е. если 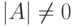$|A|\neq 0$ ) это единственное решение (k_1,...,k_n) имеет следующий вид для j=1,...,n :
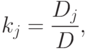$k_j = \frac{D_j}{D},$
где
$D=|A|,\quad D_j = \begin{array}{@{}c@{}} \displaystyle \left| \begin{array}{cc|c|cc} \cline{3-3} a_{11} & ... & b_1 & ... & a_{1n}\\ \vdots & & \vdots & & \vdots\\ a_{n1} & ... & b_n & ... & a_{nn}\\ \cline{3-3} \end{array}\right|\\ \begin{array}{ccccc} \hphantom{a_{11}}& & \scriptstyle j & & \hphantom{a_{1n}} \end{array} \end{array} \text{ -}$
определитель, полученный из определителя |A| путем замены j -го столбца на столбец
$\begin{pmatrix} b_1\\ \vdots\\ b_n \end{pmatrix}$
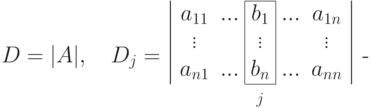свободных членов системы.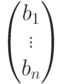

Доказательство.

Приведя элементарными преобразованиями систему к ступенчатому виду 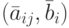$(\bar a_{ij}, \bar b_i)$ со ступенчатой матрицей 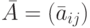$\bar A = (\bar a_{ij})$ , из критерия определенности квадратной системы имеем: система (a_ij,b_i) является определенной тогда и только тогда, когда ступенчатая матрица
$\bar A = \begin{pmatrix} \bar a_{11} & \bar a_{12} & ... & \bar a_{1n}\\ 0 & \bar a_{22} & ... & \bar a_{2n}\\ \hdotsfor{4}\\ 0 & 0 & ... & \bar a_{nn} \end{pmatrix}$
треугольная с ненулевыми элементами по диагонали,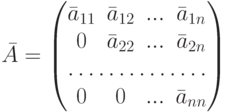 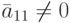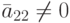$\bar a_{11}\neq 0$ , $\bar a_{22}\neq 0$ ,..., $\bar a_{nn}\neq 0$ , т. е.
$|A|=(-1)^t |\bar A| = (-1)^t \bar a_{11}... \bar a_{nn}\neq 0.$
Если (k₁,...,k_n) - единственное решение нашей системы,
$\left\{ \begin{array}{@{}l@{}} a_{11}k_1+...+a_{1j}k_j+...+a_{1n}k_n=b_1,\\ \dotfill\\ a_{n1}k_1+...+a_{nj}k_j+...+a_{nn}k_n=b_n, \end{array} \right.$
то, умножая 1 -е уравнение на A_1j, i -е - на A_ij, n -е - на A_nj и складывая, получаем
$0\cdot k_1+...+Dk_j+...+0\cdot k_n = b_1 A_{1j}+...+b_nA_{nj}=D_j.$
Итак, Dk_j=D_j,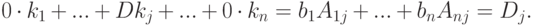 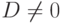$D\neq 0$ , поэтому $k_j=\frac{D_j}{D}$ .

Второе доказательство утверждения 2). Покажем, что (k₁,...,k_n), где $k_j=\frac{D_j}{D}$ , является решением.

Действительно, подставим строчку (k₁,...,k_n) в i -е уравнение $\sum\limits_{j=1}^{n}a_{ij}x_j=b_i :$

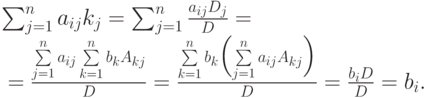
$\begin{mult} \sum_{j=1}^{n} a_{ij}k_j = \sum_{j=1}^{n} \frac{a_{ij}D_j}{D} ={} \\ {}= \frac{\sum\limits_{j=1}^{n}a_{ij}\sum\limits_{k=1}^{n}b_kA_{kj}}{D}= \frac{\sum\limits_{k=1}^{n}b_k% \Bigl(\sum\limits_{j=1}^{n}a_{ij}A_{kj}\Bigr)}{D}= \frac{b_i D}{D} = b_i. \end{mult}$

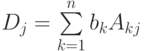Мы использовали разложение определителя D_j по j -му столбцу $D_j=\sum\limits_{k=1}^{n}b_kA_{kj}$ , а также при k=i разложение 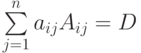$\sum\limits_{j=1}^{n}a_{ij}A_{ij}=D$ и при $k\neq i$ фальшивое разложение $\smash[t]{\sum\limits_{j=1}^{n}a_{ij}A_{kj}}=0$ .

Из теоремы Крамера можно вывести полезные следствия.

Следствие 6.8.17. Если квадратная система линейных уравнений ( n уравнений с n неизвестными) не имеет решения, то определитель матрицы ее коэффициентов равен нулю.

Доказательство. Если $|A|=|(a_{ij})|\neq 0$ , то по правилу Крамера система имеет решение.

Следствие 6.8.18. Если квадратная система линейных уравнений ( n уравнений с n неизвестными) имеет более чем одно решение, то определитель матрицы ее коэффициентов равен нулю.

Доказательство. Если $|A|=|(a_{ij})|\neq 0$ , то по правилу Крамера система имеет единственное решение.

Следствие 6.8.19. Однородная квадратная система линейных уравнений ( n уравнений с n неизвестными) имеет ненулевое решение тогда и только тогда, когда определитель матрицы ее коэффициентов равен нулю.

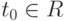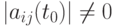Следствие 6.8.20. Если коэффициенты квадратной системы a_ij(t) и свободные члены b_i(t) являются непрерывными функциями от t, то в силу правила Крамера компоненты k_j решения (k₁,...,k_n) являются рациональными дробями от переменных {a_ij,b_i} с целыми коэффициентами и поэтому являются непрерывными функциями от t в некоторой окрестности точки $t_0\in R$ , где $|a_{ij}(t_0)|\neq 0$ .

Задача 6.8.21.Пусть 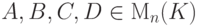$A,B,C,D\in\mM_n(K)$ . Тогда

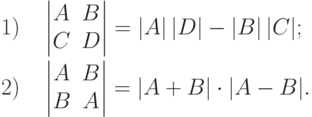
$\begin{alignat*}{2} & 1) & \quad & \begin{vmatrix} A & B\\ C & D \end{vmatrix} = |A|\,|D| - |B|\,|C|;\\ & 2) && \begin{vmatrix} A & B\\ B & A \end{vmatrix} = |A+B|\cdot |A-B|. \end{alignat*}$

Задача 6.8.22. Показать (разлагая по последнему столбцу), что

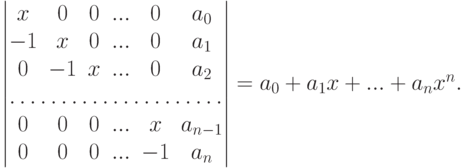
$\begin{vmatrix} \phm x & \phm 0 & 0 & ... & \phm 0 & a_0\\ -1 & \phm x & 0 & ... & \phm 0 & a_1\\ \phm 0 & -1 & x & ... & \phm 0 & a_2\\ \hdotsfor{6}\\ \phm 0 & \phm 0 & 0 & ... & \phm x & a_{n-1}\\ \phm 0 & \phm 0 & 0 & ... & -1 & a_n \end{vmatrix} = a_0+a_1x+...+a_nx^n.$

Задача 6.8.23. Пусть f(x)=(c₁-x)(c₂-x)... (c_n-x), 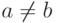$a\neq b$ . Тогда

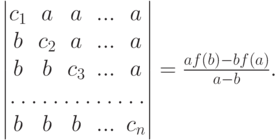
$\begin{vmatrix} c_1 & a & a & ... & a\\ b & c_2 & a & ... & a\\ b & b & c_3 & ... & a\\ \hdotsfor{5}\\ b & b & b & ... & c_n \end{vmatrix} = \frac{af(b)-bf(a)}{a-b}.$

Задача 6.8.24. Вычислить определитель порядка n

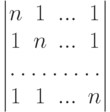
$\begin{vmatrix} n & 1 & ... & 1 \\ 1 & n & ... & 1 \\ \hdotsfor{4} \\ 1 & 1 & ... & n \end{vmatrix}$

(элементы на главной диагонали равны n, все остальные элементы равны 1 ).

Ответ (2n-1)(n-1)^{n-1}.

Задача 6.8.25. Доказать (разлагая по строке и получая рекуррентное соотношение), что

$\begin{vmatrix} a & 0 & ... & 0 & b\\ 0 & a & ... & b & 0\\ \hdotsfor{5}\\ 0 & b & ... & a & 0\\ b & 0 & ... & 0 & a \end{vmatrix} = (a^2-b^2)^k,$

где n=2k - размер матрицы.

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Вычисление определителей

Вопросы и ответы